干支が60通りである理由を分かりやすく解説！なぜ120じゃない？

干支って不思議ですね。十二支と十干の組み合わせが60通りでなので、60年で暦が還ってくる「還暦」なんて昔の人の考えって凄いですね。

十二支と十干を合わせて「十干十二支」というのが正しいそうです（私も調べていて初めて知りました！）。

でも素朴な疑問として、「十干と十二支なのに120通りにならないのはなぜ？」って思ったことはありませんか？

言われてみれば変ですよね。なぜ半分の60通りなのか？どこかに誤魔化しがあるんじゃないのか？なんて勘ぐってしまいそうです。

そこで、分かりやすくするために図を交えて解説していきたいと思います！

ぜひ最後までお付き合い下さいね。

 

十干十二支の組み合わせが60通りである理由

十干と十二支の組み合わせは60通りで全てです。

その理由をあえて言葉にすると、「数に二つのずれがある為、出会わない組み合わせがあるから」とでも表現するほかありません。

数学的に表現するならば、「この場合の組み合わせはかけ算ではなく最小公倍数になるから」とも言えます。

これでもまだ納得できない人も多いはず。「でも十干と十二支だから10×12で120通りになるんじゃないの？」と直感的には思ってしまいます。実は私もそう思っていました。

そこで、以下に図を使って解説していきたいと思います。この方がずっと分かりやすいので、是非続きをご覧下さいね。

図で分かりやすく解説

以下に十二支と十干が60通りとなる事を図解していきます。

便宜上、十二支のほうに合わせて12年を5巡するとどうなるかを見ていきましょう。「仮の年」としたのはあくまで分かりやすくするためで、実際の西暦とは異なっていますのでご注意を。

それではまず1年目から12年目までです。

 

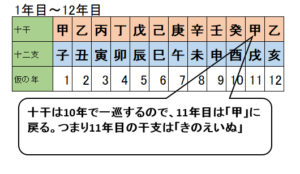
11年目には十干は2巡目に入り、「甲」となります。つまり11年目は「甲戌＝きのえいぬ」の年になります。

続けて13年目から24年目です。

 

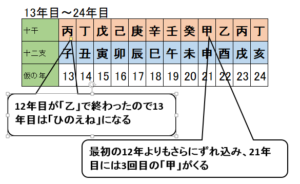
12年目は十干が「乙」でしたので、13年目は「丙」となります。だから13年目の年は「丙子＝ひのえね」となりますね。

そいて当然ながら、最初の図よりもさらにずれ込み、21年目には十干の3巡目が始まります。このようにどんどんずれていきます。

このあたりで「おや？」と思った人は鋭い！「丙」は最初は「寅」との組み合わせだったのに、十干の2巡目、つまり13年目には「丑」をすっ飛ばして「子」との組み合わせになっています！

同じ視点で見てみると、他の十干も全て十二支を一つずつ飛ばしていることが分かりますね。

さてそれではここまで飛ばされた組み合わせがこれから出会うことがあるのか？どきどきしながら続きを見てみましょう。

25年目からは全てまとめて見てみましょう。

 

 

 

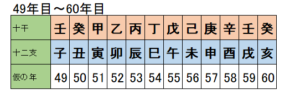
このように、60年目で十干の最後の「癸」と十二支の最後の「亥」が出会って「癸亥＝みずのとい」の年となり、61年目は1年目と同じ組み合わせに戻ります。

上で触れた「丙」と「丑」は結局のところ出会うことなく最初に戻ってしまいました。

つまりこれが全ての組み合わせなのです。見事に60通りで完結しましたね！

これでもまだ納得できない人もいるでしょう。そんな人はさらに簡単にして、「四干六支」について考えてみましょう。

 

仮に「四干六支」だとしたらこうなる

十干十二支だと数が多いので、簡略化バージョンとして「四干六支」として考えてみましょう。

「四干」は「甲・乙・丙・丁」の四つです。「六支」は「子・丑・寅・卯・辰・巳」の六つとします。

単純にかけ算をすると4×6で24通りありそうです。でも4と6の最小公倍数は12となり、やはり半分の12通りの組み合わせになります。

果たしてどちらが正しいのか、やはり図で見てみましょう。

 

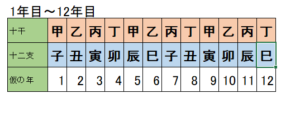
ご覧の通り、12年目で四干の最後の「丁」と六支の最後の「巳」が出会いました。つまりこの組み合わせが全てで、13年目からは1年目に戻ることになります。

結論としては、やはり組み合わせの数は最小公倍数になる事が分かりますね。

まとめ

いかがでしたか？十干と十二支の組み合わせが60通りになる謎の答はこれでスッキリしたでしょうか？

私自身も数学は大の苦手なので、最初はなかなか理解できませんでしたが、こういう表を自分で作って行くうちに成る程と腑に落ちた感もあります。

それでは今回の記事の内容をおさらいしておきましょう

これであなたも周りの人に胸を張って説明できますね！

最後までお付き合いいただきありがとうございました。